Não Decore Fórmulas: Aprenda a Raciocinar e Fique Mais Inteligente

A Armadilha de Decorar Fórmulas

Decorar fórmulas pode parecer um atalho, mas é uma armadilha. Quando você se depara com uma prova ou situação nova, qualquer variação do problema pode te deixar travado. Isso acontece porque você não entendeu o conceito, apenas memorizou um "caminho decorado" que não se adapta.

A matemática não foi feita para ser decorada. Ela foi feita para ser compreendida, explorada e internalizada.

Entender é o Caminho Mais Rápido (e Duradouro)

Quando você entende de onde vem uma fórmula, você consegue:

• Resolver problemas de formas diferentes.

• Adaptar seu raciocínio a questões novas.

• Reter o conhecimento por mais tempo.

• Desenvolver inteligência matemática, que é a capacidade de pensar logicamente, conectar ideias e resolver problemas complexos.

Vou te mostrar alguns exemplos práticos...

Exemplo 1: Equação do Segundo Grau com Produtos Notáveis e Completação de Quadrado

Considere a equação: x²+6x+5=0

A forma mais geral de resolver uma equação do 2º grau, sem ter que recorrer à fórmula de Bhaskara, é utilizando o produto notável

(x+a)²=x²+2ax+a²

para transformar a equação:

x²+6x = -5

x²+6x+9=-5+9

x²+6x+9=4

(x+3)²=4

x+3=±2

x=−1 ou x=−5

Antes que você pergunte, sim, você sempre pode seguir esse caminho para resolver qualquer equação. Isso reforça o entendimento e amplia sua capacidade de resolver equações com autonomia.

Exemplo 2: Área de um Triângulo com os Lados (Sem Fórmula de Herón)

A fórmula de Heron é longa e não intuitiva. Mas, com raciocínio geométrico, você pode buscar uma estratégia mais visual:

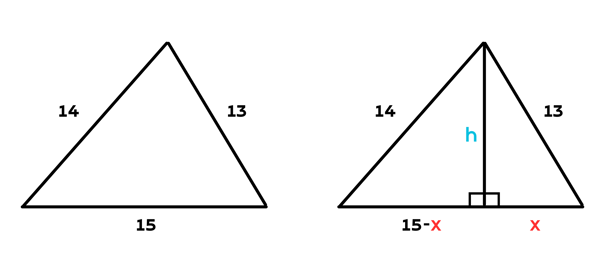
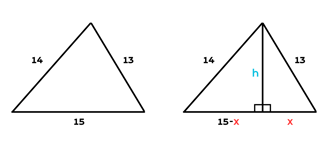
Imagine um triângulo com lados 13, 14 e 15:

Ao traçar a altura em relação a qualquer lado (dica: opte para o maior lado ser a base) você divide a base em dois segmentos e, consequentemente, surgem agora dois triângulos retângulos na imagem. Agora basta aplicar o Teorema de Pitágoras para cada triângulo e resolver o sistema:

14² = h² + (15-x)²

13² = h² + x²

Após encontrar a altura h, é só utilizar a ideia básica de área de triângulo: b.h/2 e você encontrará a área.

Exemplo 3: Combinação Usando o Princípio Multiplicativo

Ao invés de decorar a fórmula de combinação C(n,k)=n!k!/(n−k)!, pense no raciocínio por trás da ideia:

"De quantas formas posso escolher 3 pessoas entre 5?"

Use o princípio multiplicativo:

• 5 opções para a primeira pessoa,

• 4 para a segunda,

• 3 para a terceira: 5×4×3=60

Mas como a ordem não importa, dividimos pelo número de formas de organizar 3 pessoas: 3!=6.

Assim, 60/6 = 10 maneiras distintas de escolher 3 pessoas entre 5.

Com esse raciocínio, você entende o conceito de combinação sem depender da fórmula decorada.

Aprendizado Profundo Desenvolve Sua Inteligência

Estudar dessa forma ativa estimula seu córtex pré-frontal, área do cérebro ligada ao pensamento analítico e tomada de decisão. Em outras palavras: quanto mais você entende, mais inteligente você se torna.

• Você melhora a memória de longo prazo.

• Você aumenta sua criatividade para resolver problemas.

• Você ganha autoconfiança nos estudos e nas provas.

Conclusão: Chega de Decoração, Comece a Pensar!

Estudar matemática com foco em compreensão e raciocínio é mais eficiente, mais prazeroso e mais duradouro. Chega de decorar fórmulas que você esquece no dia seguinte. Comece a explorar caminhos, a entender o "porquê" por trás de cada passo e veja sua inteligência se transformar.

Quer aprender matemática de verdade, com método e profundidade? Conheça os cursos da Base de Titânio e fortaleça sua base com raciocínio e autonomia!